【课题推荐发表期刊】

【课题背景】

矩阵是数学的一个基本概念，在生活中有广泛应用。多体约化矩阵到部分矩阵的映射是一个极具挑战性的研究领域，它不仅要求对量子信息和量子多体系统有深入的理解，还要求掌握先进的计算技术。研究多体约化矩阵到部分矩阵的映射能够揭示量子系统中子系统间的纠缠特性和相互作用，同时为量子信息科技的研究提供理论基础和技术手段。

本课题将基于矩阵和线性代数的基础知识，譬如方阵，对角阵，可逆阵，线性相关等，开展相关前沿公开问题的应用。

【课题方向参考】

研究多体约化矩阵和单体约化（部分）矩阵等集合，使得这两个集合之间形成映射关系，并研究映射是单射或者满射，以及如何构建相关子集。

【适合人群】

数学、物理、信息、计算机等相关专业的高年级本科生、硕士研究生，具备初步的矩阵等相关基础知识。

【课题收获】

• 高质量论文一篇（SCI定向期刊）

• SCI期刊或中文核心期刊投递与发表指导

• 结业证书

【导师介绍】

陈老师，985高校博士生导师

• 长期担任量子物理，理论物理，数学物理，信息论领域顶级期刊的审稿人；

• 研究方向：量子信息、量子纠缠、态可区分性、矩阵数学等；

• 共发表SCI国际期刊文章100余篇，主持国家自然科学基金、北京市自然科学基金等项目多项，并担任项目评审专家

• 具备丰富的英文写作经验和学术指导经验。

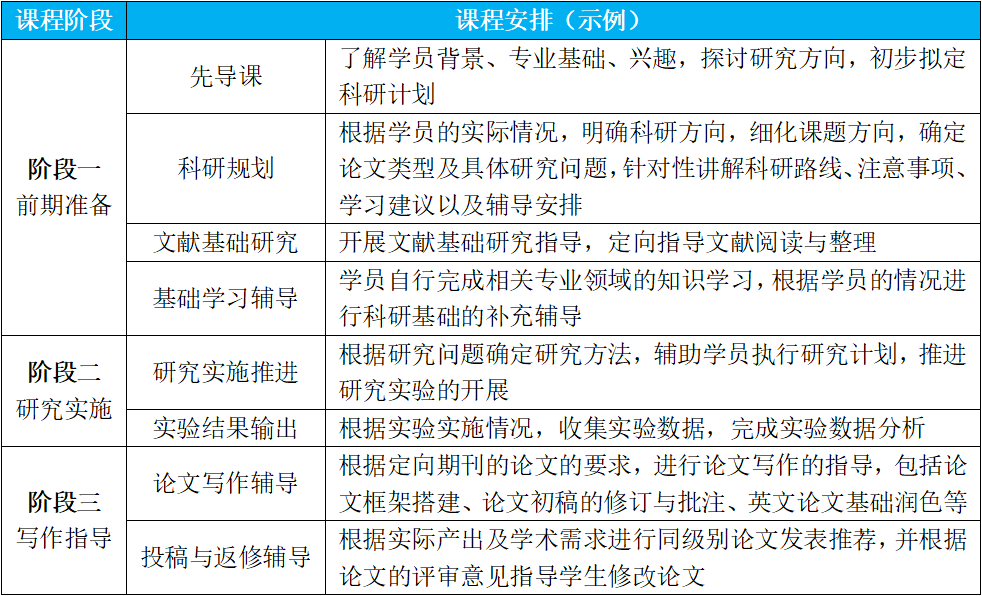
【课题安排】

研究周期预估六个月左右，具体视学员情况调整

【推荐阅读】

• 2017 Quantum state tomography via reduced density matrices