课程
施密特秩三的复哈达玛矩阵的刻画
本课题将开展施密特秩三复哈达玛矩阵和受控矩阵的关系的研究，目标是对秩三复哈达玛矩阵进行刻画。
理科
代数
施密特秩三
复哈达玛矩阵
申请匹配
咨询客服分享给朋友: 
【课题推荐发表期刊】
【课题背景】
施密特秩三指的是矩阵具有特殊的直和分解形式，这种结构使得矩阵具有某些独特的代数性质。对于复哈达玛矩阵而言，施密特秩三条件进一步限定了其结构和存在性，从而成为研究的重点。哈达玛矩阵最初在实数域上被广泛研究并应用于各种科学和工程领域。随着对复数域上的哈达玛矩阵的兴趣增加，学者开始探索其在复杂系统中的潜在应用，尤其是在信号处理和量子计算等领域。
本课题将围绕哈达玛矩阵定义展开，通过学习和研究矩阵的转置和计算、矩阵的克罗内克积、施密特秩、幺正矩阵群、排列群、复排列群、线性映射、满射和单射等概念，开展施密特秩三复哈达玛矩阵和受控矩阵的关系的研究，目标是对秩三复哈达玛矩阵进行刻画，得出其矩阵元的参数表示，从而对六阶复哈达玛矩阵这个古老的问题形成新的贡献。
【课题方向参考】
哈达玛矩阵定义和计算
克罗内克积中的可交换矩阵
矩阵的施密特秩定义和计算，和受控矩阵的关系
幺正矩阵的定义，群的定义，排列群和复排列群
判断映射的单射
【适合人群】
数学、物理、信息、计算机等相关专业的高年级本科生、硕士研究生，具备初步的矩阵等相关基础知识。
【课题收获】
高质量论文一篇（SCI定向期刊）
SCI期刊或中文核心期刊投递与发表指导
结业证书
【导师介绍】
陈老师，985高校博士生导师
长期担任量子物理，理论物理，数学物理，信息论领域顶级期刊的审稿人；
研究方向：量子信息、量子纠缠、态可区分性、矩阵数学等；
共发表SCI国际期刊文章100余篇，主持国家自然科学基金、北京市自然科学基金等项目多项，并担任项目评审专家
具备丰富的英文写作经验和学术指导经验。
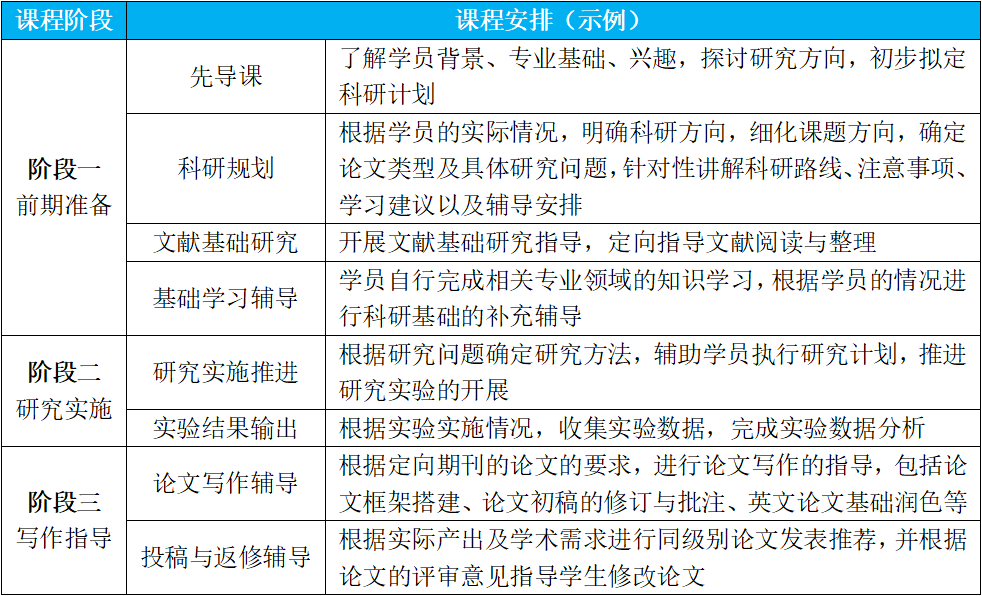
【课题安排】
研究周期预估六个月左右，具体视学员情况调整
【推荐阅读】
立即添加好友，了解更多
