【课题推荐发表期刊】

【课题背景】

矩阵的转置（transpose）是算子代数一个基本概念，它是一个线性正映射（positive map）但不是完全正映射（completely positive map）。矩阵转置映射是应用数学和代数领域的一个基本问题，在过去几十年中得到了大量研究，并仍然是当前的业界关注重点，特别是在90年代兴起的量子信息领域中和多体半正定矩阵产生了深刻的联系。

本课题将分析多体半正定矩阵的部分转置的半正定性等问题，通过研究矩阵转置和半正定矩阵的定义，推广到多体系统部分转置。可以应用于量子计算，量子测量，量子隐形传输协议等量子信息基本概念和任务。

【课题方向参考】

多体半正定矩阵的部分转置的半正定性的相关问题。

【适合人群】

数学、物理、信息、计算机等相关专业的高年级本科生、硕士研究生，具备初步的矩阵等相关基础知识。

【课题收获】

• 高质量论文一篇（SCI定向期刊）

• SCI期刊投递与发表指导

• 丘成桐赛（数学）或其他竞赛指导

• 结业证书

【导师介绍】

陈老师，985高校博士生导师

• 长期担任量子物理，理论物理，数学物理，信息论领域顶级期刊的审稿人；

• 研究方向：量子信息、量子纠缠、态可区分性、矩阵数学等；

• 共发表SCI国际期刊文章100余篇，主持国家自然科学基金、北京市自然科学基金等项目多项，并担任项目评审专家

• 具备丰富的英文写作经验和学术指导经验。

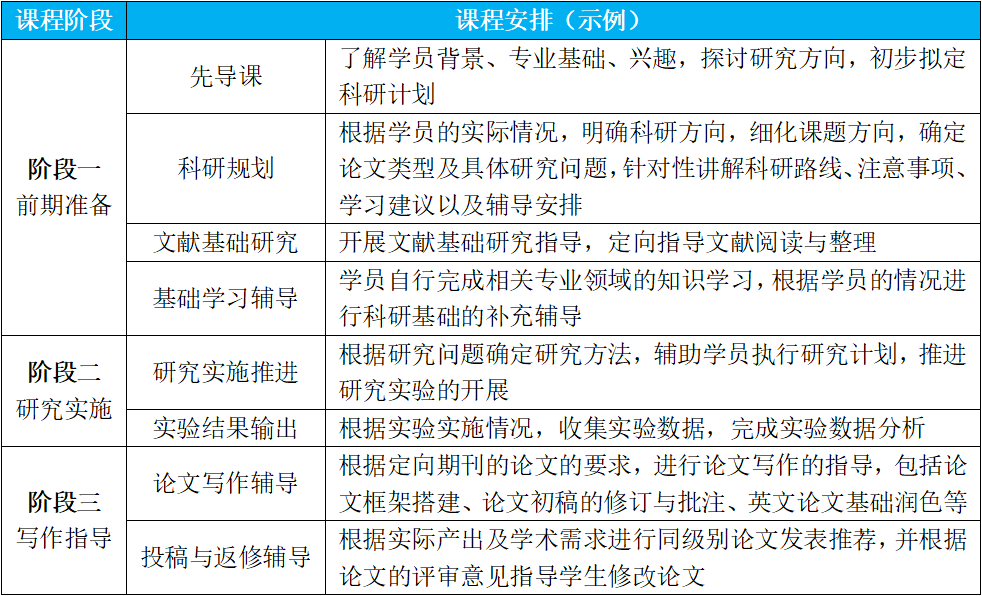
【课题安排】

研究周期预估六个月左右，具体视学员情况调整

【推荐阅读】

• 2017 Separability problem for multipartite states of rank at most 4